Τη χρυσή τομή την έχουμε ακούσει όλοι, τη χρησιμοποιούμε σαν έκφραση,και ομολογουμένως εξάπτει πάντα την περιέργειά μας. Λίγοι ωστόσο γνωρίζουμε τη θαυμαστή εννοιακή της ύπαρξη και τον σημαντικό ρόλο που διαδραμάτισε στην ιστορική πορεία του ανθρώπινου είδους και σε ό,τι με δέος αντιμετωπίζουμε, περιβεβλημένο με μυστήριο πολλές φορές, και περιλαμβάνει ο πλανήτης που κατοικούμε και, ασφαλώς, κατά έναν ανεξήγητο τρόπο, τη συναντάμε να εφαρμόζεται κατ’ επέκταση σε ολόκληρο τον μακρόκοσμό μας. Ο άνθρωπος θα συμπορευθεί με τον χρυσό αριθμό σε ένα μακρύ και μαγευτικό ταξίδι στην τέχνη, στην αρχιτεκτονική, στη βοτανική, στη βιολογία, στη φυσική και στα μαθηματικά. Εύλογο είναι ότι με τις προσωπικές ελλιπέστατες γνώσεις μας περί των μαθηματικών η προσέγγισή μας θα είναι κατά βάση θεωρητική, πιο απλοποιημένη, χωρίς εμπεριστατωμένες αποδείξεις της άλγεβρας και της γεωμετρίας που εδώ έχουν τον πρώτο λόγο αναμφίβολα.
Η χρυσή τομή συνίσταται από μια καθαρά μαθηματική έννοια και φυσικό επόμενο η εξήγησή της να εγείρει το ενδιαφέρον ανέκαθεν της επιστημονικής κοινότητας. Ωστόσο, αποτελεί ταυτοχρόνως και τη βάση της αρμονίας και της ομορφιάς σε όλες τις εκφάνσεις της τέχνης και της αισθητικής.
Στα Μαθηματικά, λοιπόν, δύο ποσότητες έχουν αναλογία χρυσής τομής αν ο λόγος του αθροίσματός τους προς τη μεγαλύτερη ποσότητα είναι ίσος με τον λόγο της μεγαλύτερης ποσότητας προς τη μικρότερη.
Η χρυσή τομή διαιρεί ένα ευθύγραμμο τμήμα σε σημείο τέτοιο ώστε ο λόγος του μικρότερου μέρους προς το μεγαλύτερο να ισούται με τον λόγο του μεγαλύτερου προς το όλον. Είναι, δηλαδή, χωρισμός ενός ευθύγραμμου τμήματος ΑΒ σε δύο τμήματα, ένα μεγάλο α και ένα μικρό β,
Το πρόβλημα αυτό τέθηκε από τον Ευκλείδη σαν διαίρεση ευθύγραμμου τμήματος σε μέσο και άκρο λόγο. Πολλούς αιώνες αργότερα η διαίρεση αυτή θα ονομαστεί χρυσή τομή, διότι θεωρήθηκε η πλέον αρμονική διαίρεση ενός ευθύγραμμου τμήματος σε δύο άνισα μέρη, ώστε το ένα να μην είναι αισθητικά μεγαλύτερο του άλλου, δηλαδή να έχουν τόση αντίθεση μεταξύ τους ώστε να μη χάνεται η ενότητα του όλου. Το ωραιότερο ζύγισμα του ευθύγραμμου τμήματος πραγματοποιείται μόνο σε ένα σημείο, το οποίο ακολουθεί την ακόλουθη σχέση: το μεγαλύτερο τμήμα του ευθύγραμμου τμήματος πολλαπλασιασμένο με τον εαυτό του να είναι ίσο με το μικρότερο πολλαπλασιασμένο με όλο το ευθύγραμμο τμήμα.
Η κυριότερη διαπίστωση των αρχαίων Ελλήνων και όσων ασχολήθηκαν με τη χρυσή τομή είναι ότι το αποτέλεσμα είναι άρρητος αριθμός (πρόκειται περί ενός ιδανικού αριθμού, που μπορούμε να τον πλησιάσουμε σε απειροελάχιστη απόσταση, αλλά είναι αδύνατον να τον συλλάβουμε ολόκληρο). Αυτό σημαίνει πρακτικά ότι δεν είναι δυνατόν ένα μικρότερο ευθύγραμμο τμήμα να χωράει σε ένα μεγαλύτερό του ακριβώς. Η συνειδητοποίηση ότι υπάρχουν αριθμοί, όπως ο χρυσός λόγος, που τα ψηφία τους συνεχίζονται επ’ άπειρον χωρίς να εμφανίζουν επανάληψη προκάλεσε δέος στους μαθηματικούς νόες της εποχής εκείνης.
Όσον αφορά τη γεωμετρία, οι κυριότερες γεωμετρικές κατασκευές που βασίζονται στη χρυσή τομή είναι η χρυσή γωνία, το χρυσό ορθογώνιο, το χρυσό τρίγωνο και το χρυσό ορθογώνιο τρίγωνο. Χρυσό τρίγωνο λέγεται κάθε ισοσκελές τρίγωνο στο οποίο ο λόγος της μεγάλης πλευράς προς τη μικρή είναι ίσος με φ. Κάθε ισοσκελές τρίγωνο με γωνία κορυφής 36° είναι χρυσό. Το χρυσό ορθογώνιο έχει λόγο πλευρών ίσο με φ. Το σχήμα των πιστωτικών καρτών, για παράδειγμα, είναι χρυσό ορθογώνιο.
«Οι αρχαίοι Έλληνες σκέφτηκαν ότι η ομορφιά είναι η σωστή δόση και η αναλογία των αντίθετων και ότι η αρμονική διαίρεση δεν σημαίνει αναγκαστικά την ισότητα και τη συμμετρία, δηλ. μια στείρα, στατική διχοτόμηση, αλλά την επίτευξη μιας δυναμικής ισορροπίας μεταξύ δυο αρμονικών άνισων μερών. Μόνο οι φιλόσοφοι και οι μαθηματικοί μπορούσαν να συλλάβουν μια τέτοια ιδέα και να βρουν σε μια ανισότητα την ακριβή θέση μιας τέλειας αρμονίας, να γεφυρώσουν με πραγματική τάξη το χάος ανάμεσα στα δυο άκρα» (Ευαγγελόπουλος Δ., 2002:208).
Η εισαγωγή και ο υπολογισμός της χρυσής τομής λέγεται ότι έλκει την καταγωγή του από τον μέγα φιλόσοφο και μαθηματικό Πυθαγόρα (585-500 π.Χ.), στη φιλοσοφική σχολή του στον Κρότωνα, της Κάτω Ιταλίας αλλά και από τη συμβολή των μετέπειτα πυθαγορείων. Γνωρίζουμε την εντρύφηση του σπουδαίου φιλοσόφου στους αριθμούς, στη μουσική και ότι μελέτησε ενδελεχώς τα φυτά και τα ζώα καταλήγοντας στο συμπέρασμα ότι οι βασικές δυνάμεις στο Σύμπαν δύναται να εκφραστούν μέσω της γλώσσας των μαθηματικών. Μάλιστα, το μυστικό σύμβολο της σχολής των πυθαγορείων ήταν η πεντάλφα – αστεροειδές πεντάγωνο, στου οποίου τις πέντε κορυφές οι πυθαγόρειοι τοποθετούσαν τα γράμματα της λέξης «Υ-Γ-Ι-ΕΙ-Α»). Το σχήμα αυτό προκύπτει από τις διαγώνιες του κυρτού κανονικού πενταγώνου οι οποίες τέμνονται σε άκρο και μέσο λόγο και υπόκειται στην προαναφερόμενη αναλογία.
Ο αριθμός φ=1,618, ο χρυσός αριθμός, μας είναι σχεδόν άγνωστος. Η αναζήτηση της θείας αυτής αναλογίας όμως θα μας οδηγήσει στην απόλυτη τάξη και στην ομορφιά της φύσης και όλου του Σύμπαντος.
Θα τον συναντήσουμε σε πολλαπλά παραδείγματα της αρχαίας αρχιτεκτονικής: Ο Φειδίας, αρχιτέκτονας του Παρθενώνα, του καλλιμάρμαρου αυτού αριστουργήματος της ελληνικής αρχαιότητας, αξιοποίησε στο έπακρο την ιδιότητα της χρυσής τομής και κληροδότησε στην ανθρωπότητα το σύμβολο φ.
Ο Ναός του Παρθενώνα παρουσιάζει τέλεια αρμονικές αναλογίες (συμμετρία) μέχρι την παραμικρή του λεπτομέρεια. Παρότι οικοδομήθηκε πάνω στον παλαιό ναό, όλες οι κύριες διαστάσεις του ακολουθούν ένα ενιαίο σύστημα αναλογιών 4:9, το οποίο συνδυάστηκε με ένα δεύτερο σύστημα αναλογιών 3:5:8, τη γνωστή μας χρυσή τομή. Αυτό σημαίνει ότι αν πολλαπλασιάσουμε το ύψος του ναού με το 9 και το γινόμενο που θα προκύψει το διαιρέσουμε με το 4, τότε θα έχουμε βρει το πλάτος του ναού. Μολονότι ο ναός αυτός ήταν κατ’ εξαίρεση μεγαλύτερος από τους άλλους δωρικούς ναούς (με 8x17 κίονες, αντί για 6x13 που συνηθιζόταν τον 5ο αιώνα π.Χ.), οι αναλογίες του ήταν τόσο αρμονικές ώστε να του προσδίδουν εκπληκτική ομοιογένεια μορφής και μνημειώδη μεγαλοπρέπεια γεμάτη πρωτοφανή χάρη. Γι’ αυτό θα θεωρείται εις το διηνεκές παγκοσμίως το «τέλειο κτήριο».
Ο Ναός του Παρθενώνα παρουσιάζει τέλεια αρμονικές αναλογίες (συμμετρία) μέχρι την παραμικρή του λεπτομέρεια. Παρότι οικοδομήθηκε πάνω στον παλαιό ναό, όλες οι κύριες διαστάσεις του ακολουθούν ένα ενιαίο σύστημα αναλογιών 4:9, το οποίο συνδυάστηκε με ένα δεύτερο σύστημα αναλογιών 3:5:8, τη γνωστή μας χρυσή τομή. Αυτό σημαίνει ότι αν πολλαπλασιάσουμε το ύψος του ναού με το 9 και το γινόμενο που θα προκύψει το διαιρέσουμε με το 4, τότε θα έχουμε βρει το πλάτος του ναού. Μολονότι ο ναός αυτός ήταν κατ’ εξαίρεση μεγαλύτερος από τους άλλους δωρικούς ναούς (με 8x17 κίονες, αντί για 6x13 που συνηθιζόταν τον 5ο αιώνα π.Χ.), οι αναλογίες του ήταν τόσο αρμονικές ώστε να του προσδίδουν εκπληκτική ομοιογένεια μορφής και μνημειώδη μεγαλοπρέπεια γεμάτη πρωτοφανή χάρη. Γι’ αυτό θα θεωρείται εις το διηνεκές παγκοσμίως το «τέλειο κτήριο».
Εξάλλου, έρευνες μας έχουν δείξει ότι ο χρυσός αριθμός φ τηρείται και στο αμφιθέατρο της Επιδαύρου, όπως και στο Θέατρο του Διονύσου και της Δωδώνης. Και οι πυραμίδες της Αιγύπτου, όπως και πολλά άλλα αρχαία μνημεία της παγκόσμιας κληρονομιάς, θεωρείται ότι υπόκεινται στην αναλογία του χρυσού αριθμού.
Επίσης, μας είναι γνωστά τα χρυσά τρίγωνα που σχηματίζονται στις αποστάσεις των ιερών τόπων της αρχαίας Ελλάδας μεταξύ τους ακολουθώντας τον κανόνα της χρυσής τομής, όπως, π.χ., το ισοσκελές τρίγωνο μεταξύ της Ακρόπολης των Αθηνών με τον Ναό του Ποσειδώνα στο Σούνιο και τον Ναό της Αφαίας Αθηνάς στην Αίγινα.
Σε κάθε μνημείο της αρχαίας Ελλάδας (π.χ Μαντείο των Δελφών, η ιερή νήσος της Δήλου, το ιερό της Δωδώνης κ.ά,) όταν χαράξουμε κύκλο με κέντρο το μνημείο και ακτίνα ένα άλλο μνημείο, η νοητή περιφέρεια του κύκλου θα περάσει και από άλλο ένα μνημείο ή πόλη! Με κέντρο τη Δωδώνη και ακτίνα κύκλου την Αθήνα, π.χ., τότε η περιφέρεια του κύκλου θα περάσει από τη Σπάρτη! Με κέντρο τους Δελφούς και ακτίνα την Αθήνα, θα περάσει η περιφέρεια από την Ολυμπία, τη Δήλο, το Άργος και τις Μυκήνες…
Ο «Δορυφόρος», του μεγάλου εξέχοντα γλύπτη Πολύκλειτου (5ος αι. π.Χ.), γνωστός επίσης ως «Κανών», ήταν έργο-βάση που ενσάρκωνε μια σχετική πραγματεία που είχε γράψει για τις ιδανικές αναλογίες ο σπουδαίος γλύπτης. Το άγαλμα επιδεικνύει μια συμμετρία, δηλαδή τέλειες αρμονικές αναλογίες, που είναι καθαρά μαθηματικές, υπολογισμένες με μεγάλη ακρίβεια και με βάση ένα κοινό μέτρο, αντιπροσωπεύοντας το «σύνολο» των «καλύτερων» αναλογιών μιας σειράς αθλητών, ιδίως ολυμπιονικών, στους ανδριάντες των οποίων ειδικευόταν ο Πολύκλειτος. Κατά τους αρχαίους, το σύστημα των αναλογιών συνίστατο στις σύμμετρες αναλογίες των σχέσεων «δακτύλου προς δάκτυλον και συμπάντων αυτών προς τε μετακάρπιον και καρπόν, και τούτων προς πήχυν, και πήχεως προς βραχίονα, και πάντων προς πάντα».
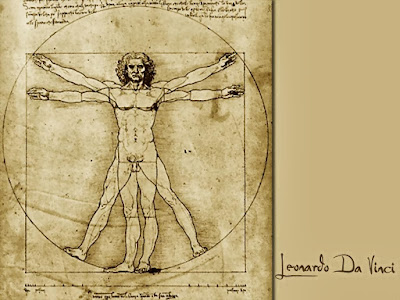
Εν κατακλείδι, οι αρχαίοι Έλληνες ήταν οι πρώτοι που ανακάλυψαν και ερεύνησαν τον αριθμό φ, οι έρευνες όμως συνεχίστηκαν άοκνα στους αιώνες που ακολούθησαν. Πολλοί σπουδαίοι μαθηματικοί και επιστήμονες ασχολήθηκαν με τον αριθμό φ από τον Μεσαίωνα έως και σήμερα... Με ονόματα όπως του Λεονάρντο ντα Βίντσι, με το διαχρονικό πρότυπο για την αρμονία του ανθρώπινου σώματος, στο έργο του ο Άνθρωπος του Βιτρούβιου, του Μαρκ Μπαρ, του αστρονόμου Γιοχάνες Κέπλερ (1571-1630), ο οποίος υπέδειξε το φ ως έναν από τους σημαντικότερους θησαυρούς της γεωμετρίας, και φυσικά του Λεονάρντο Φιμπονάτσι.
Εν κατακλείδι, οι αρχαίοι Έλληνες ήταν οι πρώτοι που ανακάλυψαν και ερεύνησαν τον αριθμό φ, οι έρευνες όμως συνεχίστηκαν άοκνα στους αιώνες που ακολούθησαν. Πολλοί σπουδαίοι μαθηματικοί και επιστήμονες ασχολήθηκαν με τον αριθμό φ από τον Μεσαίωνα έως και σήμερα... Με ονόματα όπως του Λεονάρντο ντα Βίντσι, με το διαχρονικό πρότυπο για την αρμονία του ανθρώπινου σώματος, στο έργο του ο Άνθρωπος του Βιτρούβιου, του Μαρκ Μπαρ, του αστρονόμου Γιοχάνες Κέπλερ (1571-1630), ο οποίος υπέδειξε το φ ως έναν από τους σημαντικότερους θησαυρούς της γεωμετρίας, και φυσικά του Λεονάρντο Φιμπονάτσι.
O μαθηματικός Λεονάρντο Φιμπονάτσι (1175-1240), γνωστός και ως Λεονάρντο της Πίζας, κατά τη διάρκεια των ταξιδιών του σε Αίγυπτο, Συρία, Ελλάδα και Σικελία αφομοίωσε τις μαθηματικές γνώσεις των Αράβων και πείσθηκε για την ανωτερότητα των ινδοαραβικών λογιστικών μεθόδων, που πλέον σήμερα είναι και ευρωπαϊκές. Κατά την επιστροφή του στην Πίζα δημοσίευσε το 1202 το περίφημο «Βιβλίο περί του άβακα», όπου αναλαμβάνει να μεταδώσει στη Δύση τη μαθηματική επιστήμη των Αράβων και των Ελλήνων και όπου χρησιμοποιεί σταθερά τους αραβικούς αριθμούς με το μηδέν και εισάγει τη λεγόμενη ακολουθία Φιμπονάτσι 1,1,2,3,5,8,13,21,34… , της οποίας κάθε όρος ισούται με το άθροισμα των δύο προηγούμενων όρων.
Αν φτιάξουμε μια ακολουθία με όρους τους λόγους των διαδοχικών όρων της ακολουθίας, όταν εκτελεστούν οι διαιρέσεις και όσο η ακολουθία προχωράει, τόσο το αποτέλεσμα συγκλίνει, όλο και με μεγαλύτερη ακρίβεια, προς την αποκαλούμενη χρυσή τομή, τον αριθμό φ =1,6180339887… Σε μαθηματικούς όρους, η ακολουθία των αριθμών Φιμπονάτσι προσεγγίζει το φ και είναι άρρηκτα συνδεδεμένη με τη χρυσή αναλογία.
Αν φτιάξουμε μια ακολουθία με όρους τους λόγους των διαδοχικών όρων της ακολουθίας, όταν εκτελεστούν οι διαιρέσεις και όσο η ακολουθία προχωράει, τόσο το αποτέλεσμα συγκλίνει, όλο και με μεγαλύτερη ακρίβεια, προς την αποκαλούμενη χρυσή τομή, τον αριθμό φ =1,6180339887… Σε μαθηματικούς όρους, η ακολουθία των αριθμών Φιμπονάτσι προσεγγίζει το φ και είναι άρρηκτα συνδεδεμένη με τη χρυσή αναλογία.
Οι αριθμοί Φιμπονάτσι εμφανίζονται συχνά στη φύση, τόσο στο φυτικό όσο και στο ζωικό βασίλειο, όπως για παράδειγμα στο σώμα εντόμων και ζώων. Η συγκεκριμένη αναλογία έχει παρατηρηθεί στα φυτά, τα οποία φυσικά δεν γνωρίζουν για την ακολουθία Φιμπονάτσι, απλώς μεγαλώνουν με τον πιο πρόσφορο και αποδοτικό τρόπο. Επί παραδείγματι, ο αριθμός των πετάλων σε πολλά άνθη τις περισσότερες φορές είναι ένας αριθμός Φιμπονάτσι. Όπως, τα περισσότερα τριφύλλια έχουν τρία ή πέντε φύλλα ενώ τα τετράφυλλα τριφύλλια είναι πολύ σπάνια, οι περισσότερες μαργαρίτες έχουν 34, 55 ή 89 πέταλα που είναι αριθμοί Φιμπονάτσι. Το άγριο τριαντάφυλλο, η νεραγκούλα, ο καπουτσίνος και η ακουιλέγια εμφανίζονται συνήθως με 5 πέταλα ενώ το αστράκι και η πικραλίδα με 21. Το χρυσάνθεμο έχει συνήθως 34 πέταλα όπως και ο ηλίανθος. Το ίδιο παρατηρούμε στη διακλάδωση στα δέντρα, στη διάταξη των φύλλων σε ένα στέλεχος, στα στόμια του καρπού ενός ανανά, στην ανάπτυξη της αγκινάρας, στις σπείρες στα ανθύλλια των λουλουδιών, ή στις σπείρες στα σαλιγκάρια, που είναι χρυσές σπείρες στις περισσότερες περιπτώσεις. Ακόμη βλέπουμε εφαρμογές του χρυσού αριθμού φ και στα ζώα τα οποία τον χρησιμοποιούν είτε ως προφύλαξη, είτε τον διαθέτουν ως ιδιαίτερο χαρακτηριστικό επάνω τους.
Ένα υπαρκτό παράδειγμα όπου συναντάμε αυτή τη χρυσή ακολουθία βρίσκεται στο γενεαλογικό δέντρο κάθε κηφήνα σε ένα μελίσσι. Το εν λόγω έντομο γεννιέται από ένα μη γονιμοποιημένο αβγό της βασίλισσας, δηλαδή έχει μητέρα αλλά όχι και πατέρα. Αντιθέτως, τόσο η βασίλισσα (η μοναδική που μπορεί να κάνει αβγά) όσο και οι εργάτριες γεννιούνται από αβγά που έχουν γονιμοποιηθεί από αρσενικό. Αυτές, λοιπόν, έχουν και πατέρα και μητέρα. Επομένως, το γενεαλογικό δέντρο του κηφήνα διαμορφώνεται ως εξής: έχει 1 μητέρα, 2 παππούδες (αρσενικό και θηλυκό), 3 προπαππούδες (δύο από την οικογένεια της γιαγιάς και μία του παππού), 5 προ-προπαππούδες, 8 προ-προ-προπαππούδες και ούτω καθεξής. Το γενεαλογικό δέντρο του κηφήνα είναι μια ακολουθία Φιμπονάτσι! Και όχι μόνο αυτό. Το 1966 ο Νταγκ Γιανέγκα, από το Μουσείο Έρευνας στην Εντομολογία του Πανεπιστημίου της Καλιφόρνιας, ανακάλυψε ότι η αναλογία που υφίσταται ανάμεσα σε εργάτριες μέλισσες και κηφήνες σε ένα μελίσσι προσεγγίζει τον χρυσό αριθμό.
Η θεία αναλογία χρησιμοποιήθηκε όχι μόνο στην αρχαιότητα (κτήρια και αγγεία), αλλά και στις ημέρες μας, π.χ. στο κτήριο των Ηνωμένων Εθνών, στην κατασκευή του οποίου ο αρχιτέκτονας Λε Κορμπυζιέ ακολούθησε μια κλίμακα αναλογιών που την ονόμασε Le Modulor. Η αναλογία αυτή χρησιμοποιήθηκε όχι μόνο στην αρχιτεκτονική, αλλά και στη ζωγραφική, και το όνομά της οφείλεται στον Λεονάρντο ντα Βίντσι, που ήταν ο πρώτος που την αποκάλεσε sectio aurea, δηλαδή χρυσή τομή.
Η χρυσή τομή συνδέεται τόσο με τη φανερή όσο και με την κρυμμένη αρμονία μεταξύ δυο μερών ή του μέρους με το όλον. Να αναφέρουμε, τέλος, ότι και η μουσική δεν έμεινε ανεπηρέαστη από τη χρυσή τομή. Έχουμε άγνοια όμως αν αυτό έγινε συνειδητά ή ασυνείδητα. Παρατηρούμε και εδώ στα έργα των μεγάλων συνθετών, όπως του Μότσαρτ ή του Μπετόβεν, να υπάρχει μία διαίρεση των συνθέσεων σε λόγους χρυσής τομής.
Η χρυσή τομή συνδέεται τόσο με τη φανερή όσο και με την κρυμμένη αρμονία μεταξύ δυο μερών ή του μέρους με το όλον. Να αναφέρουμε, τέλος, ότι και η μουσική δεν έμεινε ανεπηρέαστη από τη χρυσή τομή. Έχουμε άγνοια όμως αν αυτό έγινε συνειδητά ή ασυνείδητα. Παρατηρούμε και εδώ στα έργα των μεγάλων συνθετών, όπως του Μότσαρτ ή του Μπετόβεν, να υπάρχει μία διαίρεση των συνθέσεων σε λόγους χρυσής τομής.
Ο φ έχει συσχετιστεί με τις αναλογίες του ανθρωπίνου σώματος, τους βιορυθμούς του, τον καρδιακό ρυθμό, την απόσταση των ζωτικών οργάνων μεταξύ τους. Πρώτος ο Λεονάρντο ντα Βίντσι διαπίστωσε ότι ο λόγος της απόστασης από τον ώμο μας μέχρι την άκρη των δακτύλων προς την απόσταση από τον αγκώνα μέχρι τις άκρες των δακτύλων μας είναι φ. Είναι ο ζωγράφος του οποίου το όνομα συναντάται σε κάθε ισχυρισμό της εμφάνισης του χρυσού λόγου στην τέχνη. Η συζήτηση για την χρυσή αναλογία επικεντρώνεται σε πέντε έργα του Λεονάρντο: το ημιτελές «Ο Άγιος Ιερώνυμος», τις δύο εκδοχές της «Μαντόνας των Βράχων», το σχέδιο «κεφάλι ενός γέρου» και τη «Μόνα Λίζα».
Σε λεπτομερέστερα σημεία του ανθρωπίνου σώματος μπορούμε να παρατηρήσουμε και άλλες διαιρέσεις σε χρυσό λόγο. Για παράδειγμα ο καρπός διαιρεί το χέρι από τον αγκώνα και κάτω σε λόγο χρυσής τομής, ενώ αν παρατηρήσουμε κάθε φάλαγγα του ανθρώπινου δείκτη, από το ακροδάκτυλο μέχρι τη βάση του στον καρπό είναι μεγαλύτερη από την προηγούμενή της κατά περίπου 1,618, δηλαδή περίπου κατά τον χρυσό λόγο, προσαρμοζόμενη επίσης στους αριθμούς Φιμπονάτσι 2, 3, 5 και 8.
Ο μαθηματικός Άντριαν Μπέτζαν, του Πανεπιστημίου Ντιουκ των ΗΠΑ, πιστεύει ότι η ενστικτώδης προτίμηση του ανθρώπου για σχήματα με τη χρυσή αναλογία οφείλεται στο ότι είναι πιο εύκολο για το ανθρώπινο μάτι και τον εγκέφαλο να αποτυπώσουν όλες τις σημαντικές λεπτομέρειες μιας εικόνας με την αναλογία αυτήν και όχι με άλλη. Με άλλα λόγια η χρυσή αναλογία είναι το πιο αποτελεσματικό σχήμα για το «οπτικό σκανάρισμα» από τον εγκέφαλο!
Το ίδιο ισχύει και για τον λόγο του ύψους μας προς την απόσταση του αφαλού μας από τη Γη. Ακόμη και στο θέμα της γοητείας που ασκούν κάποια πρόσωπα κρύβεται ο φ. Το ότι σε κάποιους από εμάς ταιριάζει το καπέλο ή το μούσι ή τα φουντωτά μαλλιά είναι θέμα χρυσής τομής.
Παρά τη μεγάλη ποικιλομορφία των ανθρώπινων προσώπων, η «μέση προσωπογραφία» ενός ανθρώπου που προκύπτει από την αλληλεξέταση πολλών φωτογραφιών προσώπων είναι ένα ιδανικό πρόσωπο που ακολουθεί τον κανόνα του χρυσού ορθογωνίου. Δηλαδή, μπορεί να εγγραφεί σε ένα χρυσό ορθογώνιο. Επιπλέον, μπορεί εύκολα να διαπιστωθεί ότι πολλές από τις λεπτομέρειες του προσώπου βρίσκονται σε αυστηρά καθορισμένους γεωμετρικούς τομείς ή σε σημεία που προκύπτουν από την αρμονική ανάλυση του χρυσού ορθογωνίου, ενώ ο ανθρώπινος οφθαλμός έχει την ικανότητα να εντοπίζει άμεσα ακόμη και ελάχιστες αποκλίσεις από μια τέτοια αρμονική δομή (Ghyka, 1977).
Εν συνόψει, ο φ προϋπήρχε ως αναλογία από την αρχή της δημιουργίας του Σύμπαντος και συνεχίζει να υφίσταται, ακόμη και στις διαστάσεις της Γης και της Σελήνης που είναι σε σχέση φ, σχηματίζοντας ένα χρυσό τρίγωνο. Τα λεγόμενα χρυσά σπειροειδή που βασίζονται στον φ απαντώνται στις σπείρες των οστρακοειδών, αρκετών σπειροειδών Γαλαξιών, ακόμη και στις σπείρες του DNA ή στα δακτυλικά μας αποτυπώματα. Η χρυσή τομή είναι στενά συνυφασμένη, βεβαίως, με την αίσθηση του κάλλους και της αρμονίας σε αυτόν τον μοναδικό κόσμο, τον μέγα, που τα πάντα εν σοφία εποιήθησαν – από τον άνθρωπο, τα έμβια όντα έως και το Σύμπαν ολάκερο!
Μαρίνα Μαραγκού
TEXNOGRAFIA
Πηγές:
•Σωκράτης Ντριάνκος, εγκεκριμένη διπλωματική εργασία: Άρρητοι Αριθμοί και συνεχή κλάσματα.
•Πάπυρος Λαρούς Μπριτάννικα, εκδ. ΠΑΠΥΡΟΣ.
•Λεόντειο Λύκειο Νέας Σμύρνης, ερευνητική εργασία Α’ Λυκείου: « Ο χρυσός Αριθμός Φ».
•Τοσίτσειο Αρσάκειο Α’ Γενικό Λύκειο Εκάλης, ερευνητική εργασία: Χρυσός Αριθμός Φ - Χρυσή Τομή.
•Γυμνάσιο Τεγέας Αρκαδίας, διαθεματική εργασία στα Μαθηματικά με θέμα: «Η Χρυσή Τομή και ο αριθμός φ».
•Πάπυρος Λαρούς Μπριτάννικα, εκδ. ΠΑΠΥΡΟΣ.
•Λεόντειο Λύκειο Νέας Σμύρνης, ερευνητική εργασία Α’ Λυκείου: « Ο χρυσός Αριθμός Φ».
•Τοσίτσειο Αρσάκειο Α’ Γενικό Λύκειο Εκάλης, ερευνητική εργασία: Χρυσός Αριθμός Φ - Χρυσή Τομή.
•Γυμνάσιο Τεγέας Αρκαδίας, διαθεματική εργασία στα Μαθηματικά με θέμα: «Η Χρυσή Τομή και ο αριθμός φ».










υπεροχο!!!!
ΑπάντησηΔιαγραφήΕυχαριστούμε πολύ!
ΑπάντησηΔιαγραφή